(можете помочь срочно нужно).
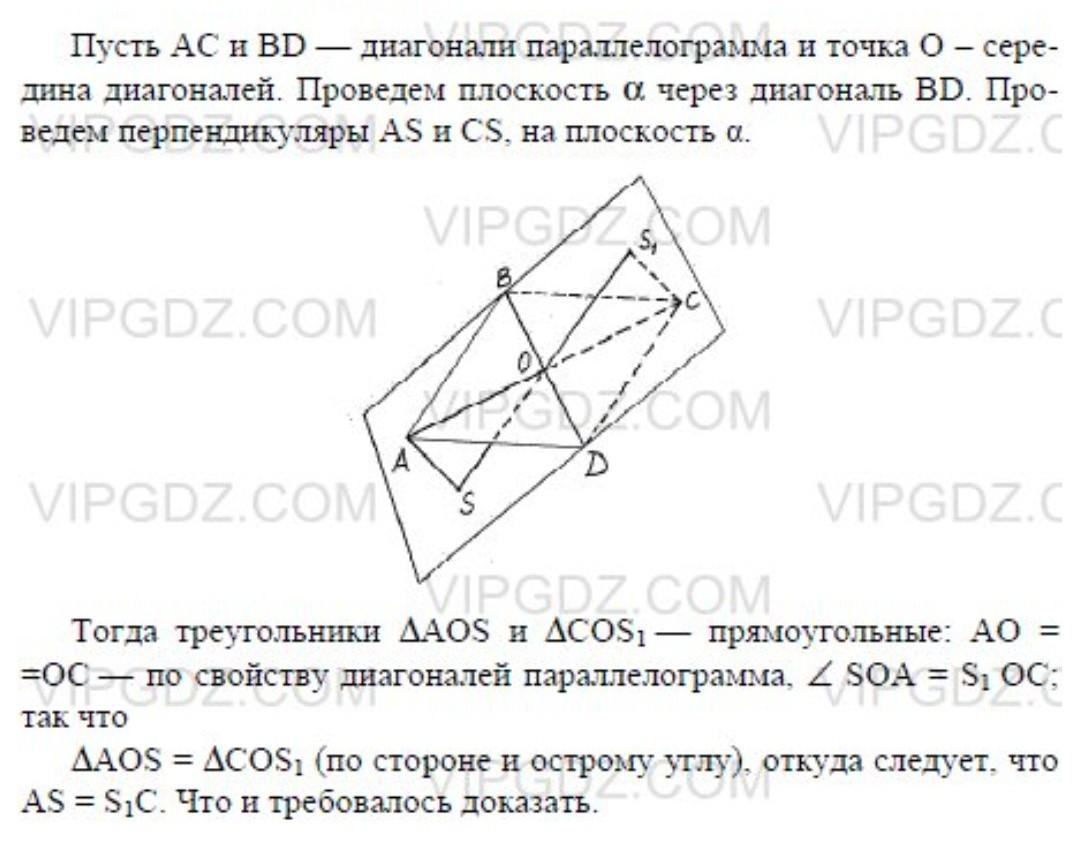
Через диагональ параллелограмма проведена плоскость. Докажите, что концы другой диагонали находятся на одинаковом расстоянии от этой плоскости.
Ответ:
Для доведення цього твердження розглянемо паралелограмм ABCD, де AC і BD - його діагоналі, і плоскість, яка проходить через діагональ AC. Позначимо точки перетину плоскості зі сторонами паралелограмма як E і F, де E - точка перетину плоскості зі стороною AB, а F - точка перетину плоскості зі стороною CD.
Для доведення, що точки перетину плоскості з іншою діагоналлю (BD) знаходяться на однаковому віддалі від плоскості, ми можемо використати властивість паралелограмма, що протилежні сторони паралельні і рівні.
Оскільки AB || CD і AB = CD, то ми можемо стверджувати, що плоскість, яка проходить через діагональ AC, також паралельна стороні CD і рівновіддалена від неї.
Таким чином, точки перетину плоскості з діагоналлю BD (точки E і F) знаходяться на однаковому віддалі від плоскості, оскільки вони лежать на паралельних сторонах паралелограмма.
Отже, ми довели, що конці іншої діагоналі паралелограмма знаходяться на однаковому віддалі від плоскості, яка проходить через першу діагональ.
Ответ:
Надеюсь помогла!♡ сек оабплпьталаоаораоао