Можете на эту помогать
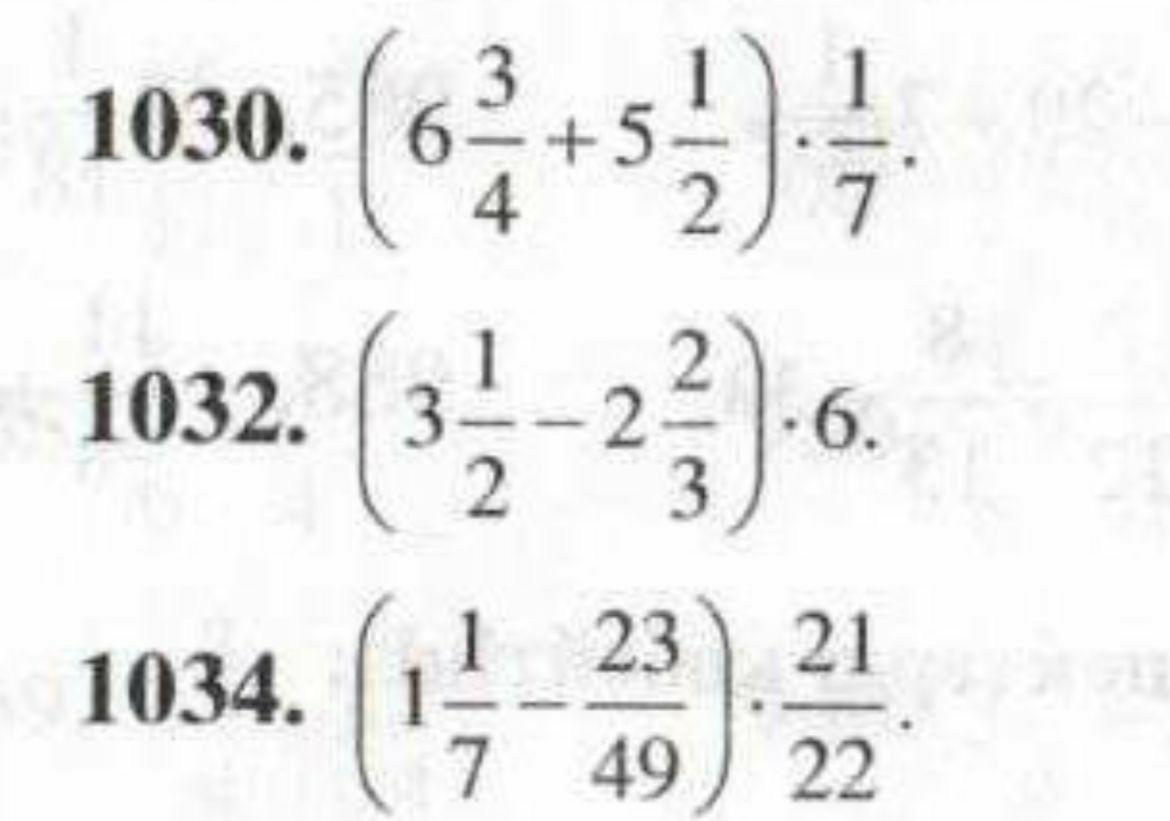
Ответ:
1030. (6 3/4 + 5 1/2) * 1/7
Для решения этого выражения, сначала нужно сложить смешанные числа в скобках.
6 3/4 + 5 1/2 = 27/4 + 11/2
Чтобы сложить эти дроби, мы должны привести их к общему знаменателю.
Общим знаменателем будет 4, так как 2 является делителем 4.
27/4 + 11/2 = (27/4)*(2/2) + (11/2)*(2/2) = 54/8 + 22/8 = 76/8 = 9 1/2
Теперь у нас получилось новое смешанное число - 9 1/2.
Следующим шагом является умножение на дробь 1/7.
9 1/2 * 1/7 = (19/2)*(1/7)
Умножаем числитель на числитель и знаменатель на знаменатель:
(19/2)*(1/7) = (19*1)/(2*7) = 19/14
Таким образом, результат выражения (6 3/4 + 5 1/2) * 1/7 равен 19/14.
1032. (3 1/2 - 2 2/3) * 6
Аналогично предыдущему примеру, начинаем с вычитания смешанных чисел в скобках.
3 1/2 - 2 2/3 = 7/2 - 8/3
Приводим дроби к общему знаменателю, который будет равен 6 (2 является делителем 6).
7/2 - 8/3 = (7/2)*(3/3) - (8/3)*(2/2) = 21/6 - 16/6 = 5/6
Теперь у нас получилась дробь 5/6.
И последний шаг - умножение на число 6.
5/6 * 6 = (5*6)/(6*1) = 30/6 = 5
Таким образом, результат выражения (3 1/2 - 2 2/3) * 6 равен 5.
1034. (1 1/7 - 23/49) * 21/22
Сначала выполняем вычитание смешанных чисел в скобках.
1 1/7 - 23/49 = 8/7 - 23/49
Дроби уже имеют общий знаменатель - 7*7 = 49.
8/7 - 23/49 = (8*7)/(7*7) - 23/49 = 56/49 - 23/49 = 33/49
Теперь у нас имеется дробь 33/49.
Следующим шагом является умножение на дробь 21/22.
33/49 * 21/22 = (33*21)/(49*22)
Производим перемножение числителей и знаменателей:
(33*21)/(49*22) = 693/1078
Таким образом, результат выражения (1 1/7 - 23/49) * 21/22 равен 693/1078.
Пошаговое объяснение:
Если не сложно сделай ответ лучшим)