Математика 1 месяц назад Lily2015

50 баллов задание на фотографии Решите уравнение​

Дополнительные материалы:
Ответ
5
OblivionFire

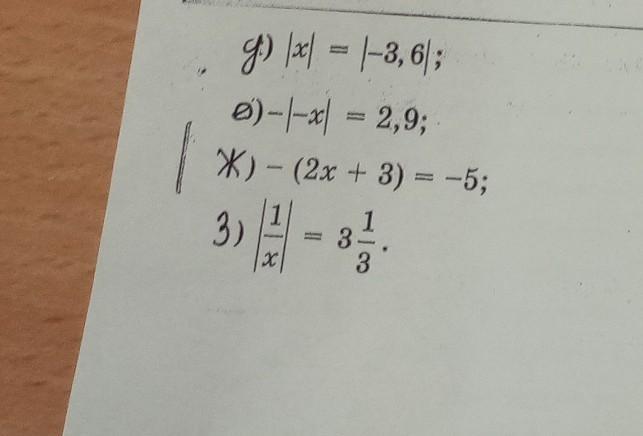
Вспомним некоторые свойства модуля:

  • \boxed{ |a|=\displaystyle\left \{ {{a,~a\geq 0} \atop {-a,~a < 0}} \right. ~;~\bigg|\frac{a}{b}\bigg|=\frac{|a|}{|b|} ,~b\ne0} .

Задание 1.

|x|=|-3,6|. Раскроем модуль в правой части уравнения ⇒ |x|=3,6. Исходя из определения модуля, имеем два решения: x=\pm3,6.

Ответ: -3,6; 3,6.

_______________________________________________

Задание 2.

-|-x|=2,9. Исходя из свойства модуля |-a|=a, получим: -|x|=2,9. Переносим "минус" в правую часть уравнения ⇒ |x|=-2,9. Любое число по модулю неотрицательно, следовательно, уравнение не имеет корней.

Ответ: x∈∅.

_____________________________________________________

Задание 3.

-(2x+3)=-5. Меняем знаки во всех частях уравнения, скобки снимаем: 2x+3=5. Решаем простое линейное уравнение с одной переменной. Переносим "3" вправо с противоположным знаком, находим разность: 2x=5-3\Rightarrow 2x=2\Rightarrow x=2:2\Rightarrow x=1.

Ответ: 1.

____________________________________________________

Задание 4.

\bigg|\dfrac{1}{x} \bigg|=3\dfrac{1}{3} . Превратим смешанное число 3\dfrac{1}{3}  в неправильную дробь. Для этого надо: умножить единицы целой части на знаменатель дробной части. К полученному произведению прибавить числитель дробной части. Полученная сумма будет числителем неправильной дроби. Знаменатель оставить без изменений. Выглядит алгебраически это вот так: a\dfrac{b}{c} =\dfrac{a\cdot c+b}{c} \Rightarrow 3\displaystyle\frac{1}{3} =\frac{10}{3} .

Преобразуем левую часть ⇒ \displaystyle\frac{|1|}{|x|} =\frac{10}{3} \Rightarrow \frac{1}{|x|} =\frac{10}{3} . Перед нами -- пропорция. Перемножим крест на крест. Основное свойство пропорции:

  • Произведение крайних членов пропорции равно произведению средних.

3\cdot1=10\cdot|x|\Rightarrow 10|x|=3. Разделим обе части уравнения на "10". Получим: |x|=\dfrac{3}{10} \Rightarrow Раскроем модуль ⇒ x=\pm0,3.

Ответ: -0,3; 0,3.

Ответ
1
NNNLLL54

Ответ:

\boxed{\ \ |x|=\left\{\begin{array}{ccc}x\ ,\ esli\ x\geq 0\ ,\\-x\, ,esli\ x<0\ .\end{array}\right\ \ \ \ ,\ \ \ |x|\geq 0\ \ }\\\\\\1)\ \ |x|=|-3,6|\ \ \ ,\ \ \ \ |-3,6|=3,6\ \ ,\\\\|x|=3,6\ \ \ \Rightarrow\ \ \ \underline {\ x_1=-3,6\ \ \ ili\ \ \ x_2=3,6\ }\\\\\\2)\ \ -|-x|=2,9\ \ \ \Rightarrow \ \ \ |-x|=-2,9\ \ \ \Rightarrow \ \ \ \underline {\ x\in \varnothing\ }  

Уравнение не имеет решений, так как   |x|\geq 0  при любых значениях "х" . Отрицательное значение модуль выражения не может принимать .

3)\ \ -(2x+3)=-5\ \ ,\ \ \ 2x+3=5\ \ \ ,\ \ \ 2x=2\ \ ,\ \ \ \underline{\ x=1\ }\\\\\\4)\ \ \Big|\dfrac{1}{x}\Big|=3\dfrac{1}{3}\\\\\dfrac{1}{x}=-\dfrac{10}{3}\ \ \ ili\ \ \ \dfrac{1}{x}=\dfrac{10}{3}\Rightarrow \ \ \ \underline {\ x_1=-0,3\ \ ili\ \ \ x_2=0,3\ }

Предыдущий вопрос
Следующий вопрос