Математика 1 год назад Lily2015

50 баллов за задание на фотографии

Дополнительные материалы:

Ответ

NNNLLL54

Ответ:

a) Так как a>0 и b>0 , то $|a|=a\ \ ,\ \ |b|=b$ .

Надо сравнить число $-a$ с числом $-|b|=-b$ .

Числа $a$ и $-a$ - это противоположные числа. То есть они находятся на одинаковом расстоянии от 0 , но по разные стороны от него . Аналогично, числа $b$ и $-b$ - противоположные числа .

Так как по условию a>b , то число $a$ находится на большем расстоянии от 0, чем число $b$ ( справа от 0 ) , а значит число $-a$ тоже находится на большем расстоянии от 0, чем число $-b$ ( слева от 0 ) .

Поэтому $-a<-b\ \ \Rightarrow \ \ \ -a<-|b|$ .

б) Числа m и n - отрицательные числа, то есть $m<0\ ,\ \ n<0$ .

Значит, $|n|=-n>0\ ,\ \ |m|=-m>0\ .$

Числа, противоположные числам $m$ и $n$ будут обозначаться как $-m$ и $-n$ , причём они положительны, то есть $-m>0$ и $-n>0$ .

По условию m>n , значит на числовой оси слева от 0 число $m$ находится ближе к 0, чем число $n$ . А поэтому справа от 0 на числовой оси число $-m$ находится к 0 ближе, чем число $-n$ .

$-n>-m\ \ \Rightarrow \ \ \ |n|>-m$

в) Аналогично рассуждая, сравним заданные числа .

$a>0\ ,\ b>0\ \ \ \Rightarrow \ \ \ \dfrac{1}{a}<\dfrac{1}{b}$ , так как чем больше знаменатель дроби, тем меньше сама дробь при равных числителях .

Если умножить неравенство на отрицательное число, то знак неравенства поменяется на противоположный, поэтому $-\dfrac{1}{a}>-\dfrac{1}{b}$ .

Так как b>0 , то и $\dfrac{1}{b}>0$ , а значит $\Big|\dfrac{1}{b}\Big|=\dfrac{1}{b}\ \ ,\ \ \ -\Big|\dfrac{1}{b}\Big|=-\dfrac{1}{b}<0$ .

Так как а>0 , то $|a|=a\ \ \Rightarrow \ \ \ \dfrac{1}{|a|}=\dfrac{1}{a}>0\ \ ,\ \ \ -\dfrac{1}{|a|}=-\dfrac{1}{a}<0$ .

Выше мы определили, что $-\dfrac{1}{a}>-\dfrac{1}{b}$ , поэтому $-\dfrac{1}{|a|}>-\Big|\dfrac{1}{b}\Big|$ .

Дополнительные материалы:

Ответ

Инкогнито

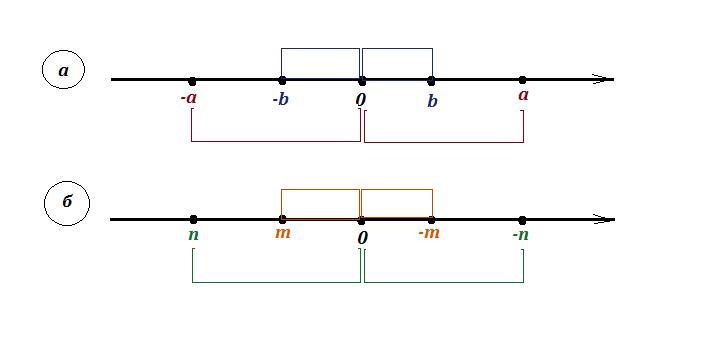
а) т.к. а>0; b>0; a>b; IbI=b; при умножении обеих частей неравенства

a>b; на минус единицу знак неравенства изменится на противоположный, т.е. -a<-b; -a<-IbI

пример : а=3, b=2, -3 <-2 ; -3<-I-2I верно.

б) m<0; n<0; m>n; то и InI, и -m- положительны, а т.к. модуль n больше модуля m, ImI=-m; то InI>-m

пример. m=-2; n=-3; I-3I>-(-2), т.е. 3>2- верно

в) -1/IаI>-1/IbI, т.к. если a>b, то IaI>IbI; 1/IaI<1/IbI ; -1/IaI> -1/IbI=-I1/bI

пример. m=3; n=2; 3>2; I3I=3; I2I=2; 1/ I3I<1/I2I=I1/2I, -1/ I3I>-1/I2I=-I1/2I,

Предыдущий вопрос

Следующий вопрос

50 баллов за задание на фотографии​

50 баллов за задание на фотографии