Алгебра 2 месяца назад petr2013

Помогите срочно решить неравенство с модулем.

Дополнительные материалы:

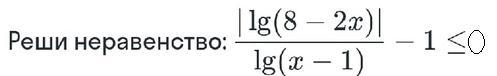
Simba2017: по моему с учетом одз модуль можно опустить..

Simba2017: тогда ответ x=[3;4)

hote: а чем промежуток (1;2) не понравился?

hote: при х= 3,9 неравенство не справедливо

Simba2017: может вы все решение напишите?

Ответ

hote

$\displaystyle \frac{|lg(8-2x)|}{lg(x-1)}-1\leq 0\\\\ODZ: \left \{ {{8-2x>0; x-1>0} \atop {lg(x-1)\neq 0}} \right. \Rightarrow\left \{ {{x<4; x>1} \atop {x\neq 2}} \right. \Rightarrow x \in (1;2)(2;4)$

1) раскроем модуль при lg(8-2x)≥0

$\displaystyle lg(8-2x)\geq 0 \Rightarrow 8-2x\geq 1 \Rightarrow x\leq 3.5$

тогда

$\displaystyle \frac{lg(8-2x)}{lg(x-1)}\leq 1$

$\displaystyle log_{x-1}(8-2x)\leq 1$

далее применим метод рационализации

$\displaystyle log_hF\leq 1\Rightarrow (h-1)(F-h)\leq 0$

получаем

$\displaystyle (x-1-1)(8-2x-x+1)\leq 0\\\\(x-2)(9-3x)\leq 0$

и метод интервалов

x=2; x=3

___-_____2__+____3___-___

1 по условию 3,5

тогда в первом случае x∈ (1;2)∪ [3;3.5]

2) раскроем модуль lg(8-2x)<0

$\displaystyle lg(8-2x)<0 \Rightarrow 8-2x<1\Rightarrow x>3.5$

тогда

$\displaystyle \frac{-lg(8-2x)}{lg(x-1)}\leq 1\\\\-log_{x-1}(8-2x)\leq 1\\\\log_{x-1}\frac{1}{8-2x}\leq 1$

метод рационализации

$\displaystyle (x-1-1)(\frac{1}{8-2x}-(x-1))\leq 0\\\\(x-2)\bigg(\frac{1-(x-1)(8-2x)}{8-2x}\bigg)\leq 0\\\\(x-2)(\frac{1-(-2x^2+10x-8)}{8-2x})\leq 0\\\\(x-2)(\frac{2x^2-10x+9}{8-2x})\leq 0$

x=2; x≠4; x= 2.5 ±0,5√7 (это х ≈ 3,82 и х≈1,17)

_-___2,5-√7___+___2_____-______2,5+0,5√7__+____4___-___

3,5 по условию 4

тогда во втором случае х∈(3,5; 2.5+0.5√7]

3) и теперь все объединяем

х∈ (1;2)∪ [3; 2.5+0.5√7]

Simba2017: вы молодец! не зачтите за наглость, но там еще было одно похоже задание, если встретите-решите его для нас!

Simba2017: я еще с такими примерами на "вы"))))))

Предыдущий вопрос

Следующий вопрос