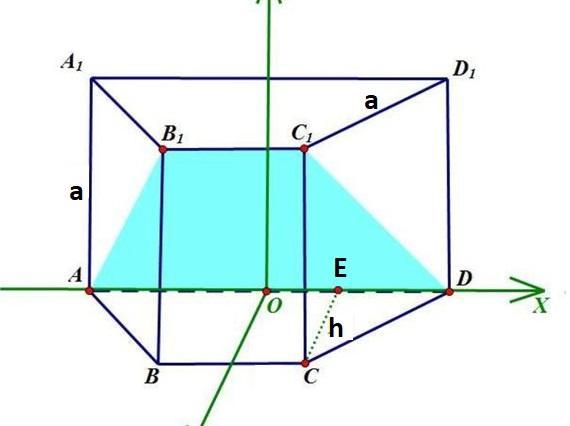
Геометрия 1 год назад KoteykaMilasha

Основание прямой призмы - равнобедренная трапеция, одно из оснований которой в три раза больше другого. Непараллельные боковые грани призмы - квадраты со стороной 4 см. Площадь боковой поверхности призмы 64 см^2. Вычислите объем призмы.

Ответ

vlad210170

Ответ:

Vпризм = 32√3

Объяснение:

дано: АВСDА1В1С1D1-призма

АВСД = равнобокая трапеция

АА1ВВ1=СС1DD1-квадрат, a=4

3ВС = АВ,

Vприз=?

Vприз = Sосн* h;

обозначим "х" = ВС - малое основание трапеции , тогда АВ=3х

Рпризм= 4х+2а

Sбок= (4х+2а) * а; $x=\frac{1}{4a} *(Sbok} - 2a^2)$

$x=\frac{1}{4*4} *(64 - 2*4^2)=\frac{1}{16} * 32 =2$ = BC=B1C1

AD = A1D1 = 3 * 2 = 6

Sтрап = $\frac{BC+AD}{2} * h$ из ΔСЕD СЕ=h = √(CD^2 - DE^2)

$DE = \frac{AD-BC}{2}=\frac{6-2}{2} =2$

h = $\sqrt{4^2-2^2} = \sqrt{(4+2)(4-2)} = 2\sqrt{3}$

Vпризм = $\frac{2+6}{2} *2\sqrt{3}*4= 32\sqrt{3}$

Дополнительные материалы: