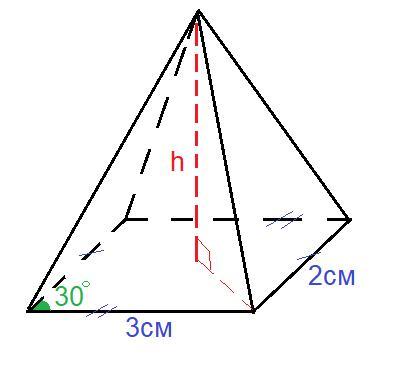
Математика 2 месяца назад annaplatonova56733

объем пирамида в основании параллелограмм со сторонами 3 и 2 см и углом между ними 30° ,равен 7см^2. найти высоту пирамиды

Ответ

xERISx

Уточнение к условию задачи: объём пирамиды измеряется в кубических сантиметрах:

V = 7 см³.

В основании пирамиды - параллелограмм, площадь которого можно посчитать по формуле:

$S_o=ab\sin \alpha ,$ где

$a,b-$ соседние стороны параллелограмма,

$\alpha -$ угол между этими сторонами параллелограмма.

По условию $a=3$ см, $b=2$ см, $\alpha =30^\circ.$

$S_o=3\cdot2\cdot\sin\alpha =3\cdot 2\cdot \dfrac12=3$ см².

Объём пирамиды с основанием $S_o$ и высотой $h$ можно вычислить по формуле:

$V=\dfrac 13\cdot S_o\cdot h$

$7=\dfrac 13\cdot 3\cdot h;\ \ \ \ \boldsymbol{h=7}$ см

Ответ: 7 см.

Дополнительные материалы: